by Blake Bordelon, Abdulkadir Canatar and Cengiz Pehlevan

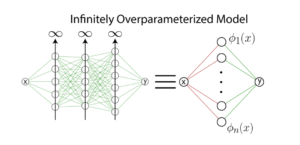
Image 1. An infinitely overparameterized neural network trained with gradient descent can be considered as kernel regression with non-linear features φ_n.

Often, we need only a few examples to learn a task, whether acquiring a new word or recognizing a new face. This number is orders of magnitude below the number of plastic synapses involved during learning. This “overparameterization” (shown in Image 1) implies that the brain is capable of fitting the same examples in many different ways and classical wisdom from statistics suggests that it can overfit (Image 2), leading to poor generalization. It must be that the brain’s neural networks carry inductive biases that allow its networks to escape the perils of overparameterization. These inductive biases must suit the learning tasks encountered during lifetime. Understanding the mechanics of how all this works is crucial for understanding how the brain can learn efficiently.

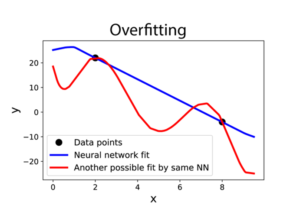
Image 2. An overparameterized network fitting two points. While it is capable of expressing more complicated functions (red), inductive bias of gradient descent leads a simpler function (blue).

Deep networks provide a test ground for understanding how neural networks can avoid overfitting. Indeed, trained deep networks have been successful models in neuroscience. They can be predictive of neural activity and provide mechanistic insight into how computations are done in the brain. Further, many practical applications of modern deep networks operate in an overparameterized regime. Therefore, we set out to understand why deep networks do not overfit.

In short, we found that deep networks exhibit a bias towards fitting data with “simple” functions (as shown in Image 2). To the extent that these simple functions align with the learning task (Image 3), sample efficient learning is possible, and we say that the network has a good inductive bias for this task. If the learning task requires fitting a “complex” function, then learning is not sample-efficient. In our work, we give precise definitions of simple and complex functions.

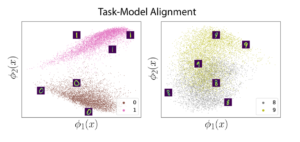
Image 3. Projections of MNIST digits along the top two features φ₁ and φ₂ of NTK for 0-1s (Left) and 8-9s (Right). Separability in this projection shows how well the task is aligned with the kernel’s features. We find that the 0-1 classification task is achieved faster than the 8-9 classification task.

More specifically, we addressed the question of overfitting for infinitely overparameterized neural networks obtained by taking the number of neurons in a layer of a network to infinity (Image 1). In this limit, (gradient descent) training of a neural network is equivalent to a popular learning model known as kernel regression. Kernel regression is the problem of finding a weighted linear combination of nonlinear feature functions to fit the provided data. Training infinitely wide neural networks correspond to performing kernel regression with a particular set of feature functions which in turn define a kernel called the Neural Tangent Kernel (NTK).

This link to kernel regression gave us an analytical handle to address the problem. We used methods from statistical physics to compute the learning curve of kernel regression not only for the Neural Tangent Kernel but for any kernel and dataset. Learning curve quantifies the average generalization error rate for kernel regression as a function of the size of the dataset. We introduced a quantitative notion of alignment between the learning task and the learning model. If the alignment is good, learning is sample-efficient. Importantly, our theory works on real data and for networks of modest width!

Our key finding was that kernel regression, and infinitely wide neural networks, exhibit a “spectral bias”, where the feature functions which account for the largest fraction of the power in the kernel can be learned most quickly as the dataset size grows. Consequently, tasks which can be expressed as a sum of these highest power modes can be learned most rapidly. The alignment of the task with these modes can be computed through simple overlaps of these special feature functions with the task function.

Overall, we found that spectral bias and task-model alignment, together, allow sample-efficient learning in kernel regression and (infinitely) overparameterized neural networks.

Abdulkadir Canatar and Blake Bordelon are PhD students in the group of Cengiz Pehlevan. Cengiz Pehlevan is an Assistant Professor of Applied Mathematics at the Harvard John A. Paulson School of Engineering and Applied Sciences.

Learn more in the original research article:
Spectral bias and task-model alignment explain generalization in kernel regression and infinitely wide neural networks. Canatar A, Bordelon B, Pehlevan C. Nat Commun. 2021 May 18;12(1):2914. doi: 10.1038/s41467-021-23103-1. PMID: 34006842; PMCID: PMC8131612.